나이브 베이즈 분류기
- 선형 모델과 매우 유사한 분류기.
- 각 특성을 개별로 취급해 파라미터 학습.
- 각각의 통계를 다 내어 취합하는 방식.
- GaussianNB
- 연속적인 데이터에서도 적용 가능
- 텍스트 데이터 분류에 주로 사용
- BernoulliNB
- 이진 데이터에 적용 가능
- 텍스트 데이터 분류에 주로 사용
- MultinomialNB
- 카운트 데이터에 적용 가능.
- 카툰트 데이터 -> 개수를 나타내는 정수형 특성 (문장에 나타난 단어의 횟수)
+ 파이썬 Numpy의 axis를 이용한 덧셈
- axis를 이용하여 배열의 축을 이용한 덧셈




axis가 증가할 수록 안쪽으로 들어감.
- 매개변수
- 매개 변수 조절만으로 정확도를 높일 수 있음.
- alpha: 모델의 복잡도를 조절 (alpha가 크면 완만해지고 복잡도 낮아짐.)
- 장, 단점
- 선형 모델로는 학습시간이 너무 오래 걸리는 매우 큰 데이터셋에 적합.
X = np.array([[0, 1, 0, 1],
[1,0, 1, 1,],
[0, 0, 0, 1],
[1, 0, 1, 0]])
y = np.array([0,1,0,1])counts = {}
for label in np.unique(y):
counts[label] = X[y == label].sum(axis = 0)
print("특성 카운트:", counts)
print("np.unique(y)=", np.unique(y))
# np.unique(y)= [0 1]
print("y == 0:", y == 0)
print("y == 1:", y == 1)
# y == 0: [ True False True False]
# y == 1: [False True False True]
print("X[y == 0]:\n", X[y == 0])
print("X[y == 1]:\n", X[y == 1])
결정 트리 (Diecision Tree)
- 분류와 회귀 문제에 널리 사용하는 모델
- 결정에 다다르기 위해 예/아니오 질문을 이어나가면서 학습.
import mglearn
mglearn.plots.plot_animal_tree()
과대적합을 막는 전략
- 사전 가지치기
- 트리 생성을 일찍 중단.
- 트리의 최대 깊이나 리프의 최대 갯수를 제한.
- 노드가 분할하기 위한 포인트의 최고 개수를 지정.
- 사후 가지치기
- 트리를 만든 후 데이터 포인트가 적은 노드를 삭제하거나 병합하는 전략.
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))
과대적합 상태
훈련 세트 정확도는 100이지만
테스트 세트 정확도가 많이 차이남 -> 과대적합 상태.
사전 가지치기 예제
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))
훈련 세트 정확도는 떨어졌지만
테스트 세트 정확도가 올라갔음!
for i in range(1,10):
tree = DecisionTreeClassifier(max_depth=i, random_state=0)
tree.fit(X_train, y_train)
print("Test Set Accuracy({}):{:.3f}".format(i,tree.score(X_test, y_test)))
for문을 이용하여 depth의 값을 변경해 정확도가 가장 높은 depth 값 찾기.
from sklearn.tree import export_graphviz
# 트리를 시각화.
# .dot -> 노드 사이의 연결을 저장해놓은 텍스트 파일
export_graphviz(tree, out_file="tree.dot", class_names=["악성","양성"],
feature_names=cancer.feature_names, impurity=False, filled=True)import graphviz
with open("tree.dot", encoding = "UTF-8") as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))from sklearn.tree import plot_tree
plt.figure(figsize=(12,6))
plot_tree(tree, class_names=["악성","양성"], feature_names=cancer.feature_names,
impurity=False, filled=True, rounded=True, fontsize=6)
plt.show()
- 트리를 시각화한다면 알고리즘 예측 과정을 이해시킬 수 있음.
- 비 전문가에게 머신러닝 알고리즘 설명하기에 좋음.
특성 중요도
- 0: 전혀 사용되지 않음
- 1: 완벽하게 타깃 클래스 예측
- 특성 중요도 전체 합: 1
L1 모델은 중요도 0을 다 지워버림.

특성과 클래스 간의 분석
- class , target, label 다 비슷한 말.
- ex) 악성, 양성
- 선형 모델의 계수와는 달리 특성의 중요도는 항상 양수
- 특성이 어떤 클래스를 지지하는지 알 수 없음.
- worst radius(높은 반지름)이 중요하다는 것을 알 수 있음.
- 높은 반지름이 양성, 악성을 의미하는지 알 수 없음.


이런 그래프로는 결정 트리를 사용하기 어려움.
선형 모델은 훈련 데이터 밖의 포인터에 대해 예측을 할 수 있음.
결정 트리 모델은 훈련 데이터 범위 밖의 포인터에 대해 예측을 할 수 없음.
외삽(extrapolation) 불가
훈련 데이터의 범위 밖의 포인터에 대해 예측을 할 수 없음.
컴퓨터 메모리 가격 동향 데이터셋
- 컴퓨터 메모리 가격 동향 데이터셋을 이용한 예제
- X축: 날짜
- Y축: 해당 년도의 랠(RAM) 1메가바이트당 가격
날짜 특성 하나만으로 2000년도 후의 가격 예측
2000년도 이전 데이터셋을 이용한 학습
두 가지 모델 비교
DecisionTreeRegressor
LinearRegression
import os
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH,"ram_price.csv"))
plt.yticks(fontname="Arial")
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("년")
plt.ylabel("가격($/Mbyte)")
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
data_train = ram_prices[ram_prices.date<2000]
data_test = ram_prices[ram_prices.date >= 2000]
X_train = data_train.date.to_numpy()[:, np.newaxis]
y_train = np.log(data_train.price)
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)
X_all = ram_prices.date.to_numpy()[:, np.newaxis]
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)plt.semilogy(data_train.date, data_train.price, label="train data")
plt.semilogy(data_test.date, data_test.price, label="test data")
plt.semilogy(ram_prices.date, price_tree, linestyle="dashed", label="tree prediction")
plt.semilogy(ram_prices.date, price_lr, linestyle="dashed", label="lr prediction")
plt.legend()
2000년 이전 데이터로 학습, 2000년 이후 데이터로 테스트
트리는 있는 데이터로 학습하기 때문에 다음 데이터는 예측 불가능.
선형 모델은 실제 2000년 이전으로 학습했어도 그 뒤 내용을 예측 가능함.
트리 예측은 외부 데이터 예측은 불가능, 데이터 안에서 예측할 수 있음.
결정 트리에서 복잡도 조절 매개변수
- 트리가 완전히 만들어지기 전에 멈추게 하는 사전 가지치기 매개 변수
- 한 가지만 사용해도 과대적합 방지 가능
- max_depth
- max_leaf_nodes
- min_samples_leaf
단점
일반화 성능이 좋지 않음 -> 사전 가지치기를 사용함에도 불구하고 과대적합되는 경향
앙상블 기법이 좋음...
결정 트리의 앙상블
- 앙상블: 여러 머신러닝 모델을 연결하여 더 강력한 모델을 만드는 기법.
- 랜덤 포레스트(Random Forest) 결정 트리
- 그래디언트 부스팅(Gradient Boosting) 결정 트리
랜덤 포레스트
- 여러 결정 트리의 묶음.
- 훈련 데이터에 과대적합 되는 문제 회피 가능
- 결정 트리의 주요 단점인 과대적합을 피할 수 있음. → (원래 트리) 결정적인 한 데이터로 정확도가 바뀔 수 있음.
1. 생성할 트리의 개수
- RandomForestRegressor나 RandomForestClassifier의 n_estimators 파라미터로 지정.
- 트리가 10개 필요하다고 가정
- 트리들은 완전히 독립적으로 생성해야 함
- 알고리즘은 각 트리가 고유하게 만들어지도록 무작위 선택 진행.
2. 부트스트랩 샘플(bootstrap sample) 생성
- n_samples 개의 데이터 포인트 중에서 무작위로 n_samples 횟수 만큼 반복 추출.
랜덤 포레스트의 트리가 조금씩 다른 데이터셋을 이용해 생성 → 트리마다 다름.
- 핵심 매개변수
- max_features
- 트리의 깊이는 낮게 설정해주는 것이 좋음.
회귀: 예측들을 평균하여 최종 예측 생성
분류: 약한 투표 전략 사용, 각 알고리즘이 가능성 있는 출력 레이블의 확률을 제공.
랜덤 포레스트 분석
two_moon 데이터셋 활용
noise -> 불규칙한 자연 데이터 넣어주기.
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)fig, axes = plt.subplots(2, 3, figsize=(20,10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
ax.set_title("트리{}".format(i))
mglearn.plots.plot_tree_partition(X, y, tree, ax=ax)
mglearn.plots.plot_2d_separator(forest, X, fill=True, ax=axes[-1,-1], alpha=.4)
axes[-1,-1].set_title("랜덤 포레스트")
mglearn.discrete_scatter(X[:,0], X[:,1],y)
5개의 트리들을 다 합친 것이 랜덤 포레스트이다.
실제 응용에서는 수백, 수천개 트리를 사용하므로 더 부드러운 결정 경계 생성 가능.
유방암 데이터셋
100개의 트리로 이루어진 랜덤 포레스트 적용하기.
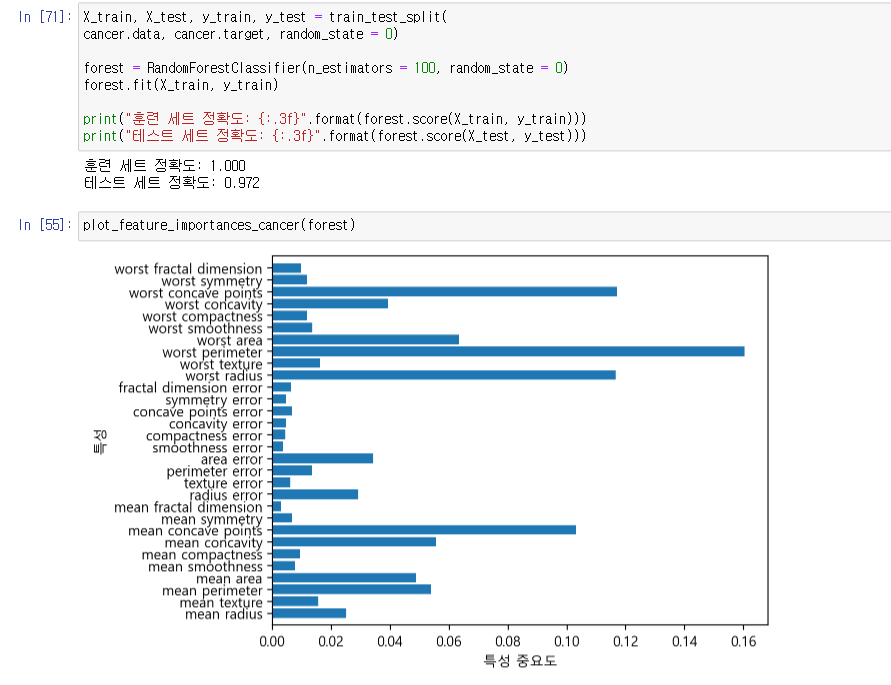

랜덤 포레스트보다 단일 트리가 적합한 경우
- 의사 결정 과정을 간소하게 표현하려면 단일 트리 사용 가능.
- 수백개의 트리를 분석하기는 어려움.
- 특성의 일부만 사용하므로 결정 트리보다 더 깊어지는 경향이 있음
- 비 전문가에세 예측 과정을 시각적으로 보여주기 위한 목적.
언어처리로는 부적합함.
텍스트 데이터 같은 고차원 데이터는 선형 모델이 좋음.
빠르게 처리 → 선형모델
적합한 정보 → 랜덤 포레스트
'ABC 부트캠프 > 머신러닝' 카테고리의 다른 글
| 20일차 - 지도학습 3 (0) | 2023.04.12 |
|---|---|
| 18일차 - 지도학습 1 (0) | 2023.04.11 |
| 17일차 - 머신러닝(ML) (0) | 2023.04.11 |



댓글